
Fun math puzzles for kids
Funny math puzzles can be an amazing way to learn mathematics in a creative manner, both for kids and adults! For those who once found math lessons at school boring, they can help look at the subject differently, even if they are teenagers, college students, or even parents teaching their kids.
What are math puzzles?
Like most puzzles, math puzzles contain some encryption, with drawings involved in them. At the same time, they require performing the corresponding operations — from simple arithmetic (addition, subtraction, multiplication, division) to construction of a system of equations. Sometimes pictures can be replaced by numbers.
To cope with the math puzzle, you need to place the mathematical signs to get the correct equality or guess the numbers that match the picture.
Why are math puzzles good for kids?
According to modern studies, kids who work on math puzzles are better at problem-solving, learning new things, and solving everyday problems. Solving such puzzles requires not only logic and attention but also the ability to count.
If you are a parent teaching your children or a teacher at primary school wishing to get your students excited about math lessons, here are some puzzles for you.
Math puzzles for kids:
Puzzle #1
Let’s look at the example of a puzzle that is solved not by replacing figures with numbers but by building equations.
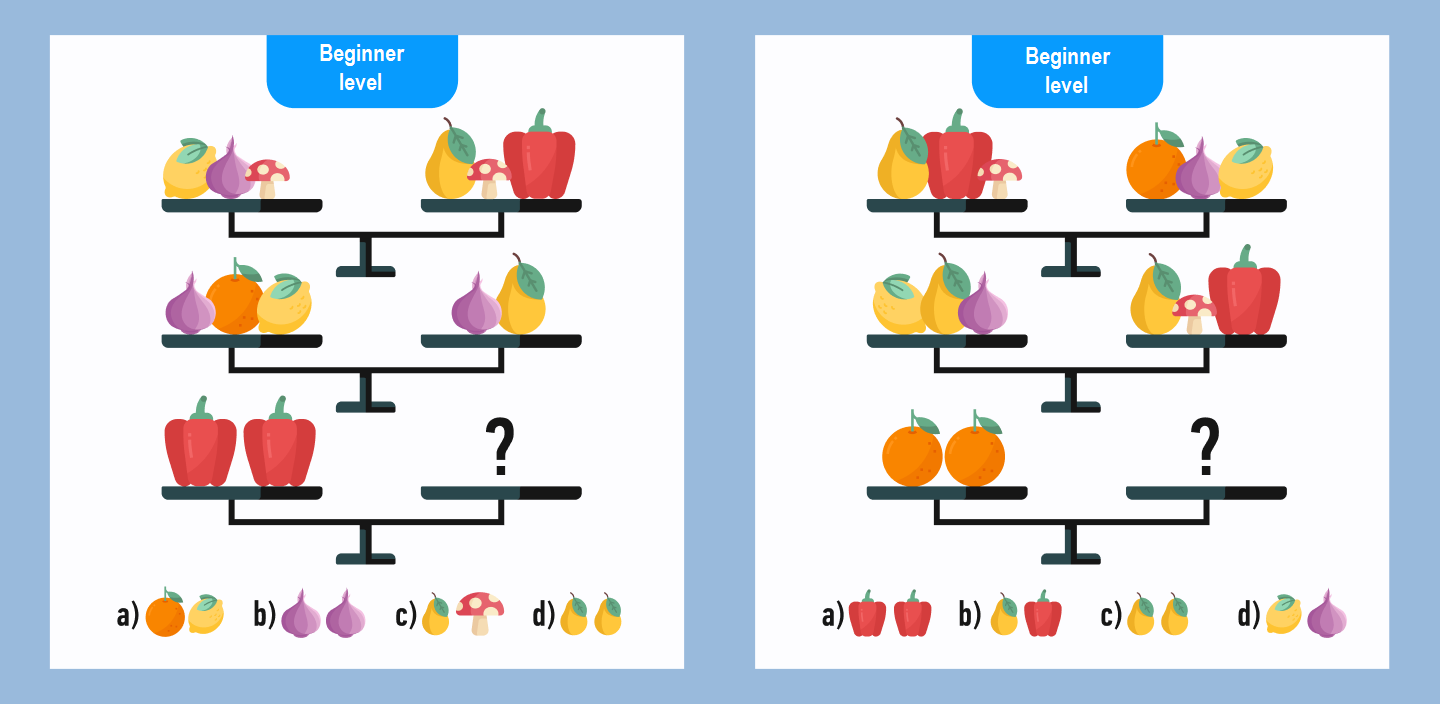
There are fruit and vegetables on the scales. In all three cases, the scales are balanced, but we don’t know what is on one of the scales in one of the three cases. You need to find which fruit or vegetables are in the last bowl. There are four possible answers.
Let’s look at the first puzzle.
Here, we need to be very attentive. Removing the repeating mushrooms from the first “equality”, we get equal pictures on the left side here and on the left side of the scales below. Therefore, we can equate the items on the two right scales: pear + pepper = onion + pear, so a pepper and an onion are equal as well. So, two peppers correspond to two onions, and the right answer is under the letter b.
If fruit and vegetables on the scales do not repeat themselves, as in this example, then you can calculate what the desired fruit is equal to, according to math rules, even though the “equation” can be quite long. To understand the principles of solving more complex “equations” that cannot be mastered without a pencil and paper, we will try to solve this in a less obvious way, but an easier one.
So, lemon + onion + mushroom + orange = pear + mushroom + pepper. Since at the end we have to calculate what the two peppers correspond to, it is logical to calculate what one is equal to. From the first equality, we can see that pepper = lemon + onion + mushroom + orange – pear – mushroom. According to mathematical laws, we can cross out the mushroom with the signs “+” and “-“. Therefore: pepper = lemon + onion + orange – pear. But from the second equality, we can see that lemon + onion + orange = onion + pear, so, lemon + orange = pear. So, we can put lemon + orange in the first “equation” instead of pear. Pepper = lemon + onion + orange – (lemon + orange). Pepper = onion. Therefore, two peppers are equal to two onions (answer b).
The second puzzle is similar, so you can try to solve it yourself.
The correct answers are:
- b for the left puzzle
- c for the right puzzle.
If the entry-level puzzles were easy for you, feel free to move on to more difficult ones!
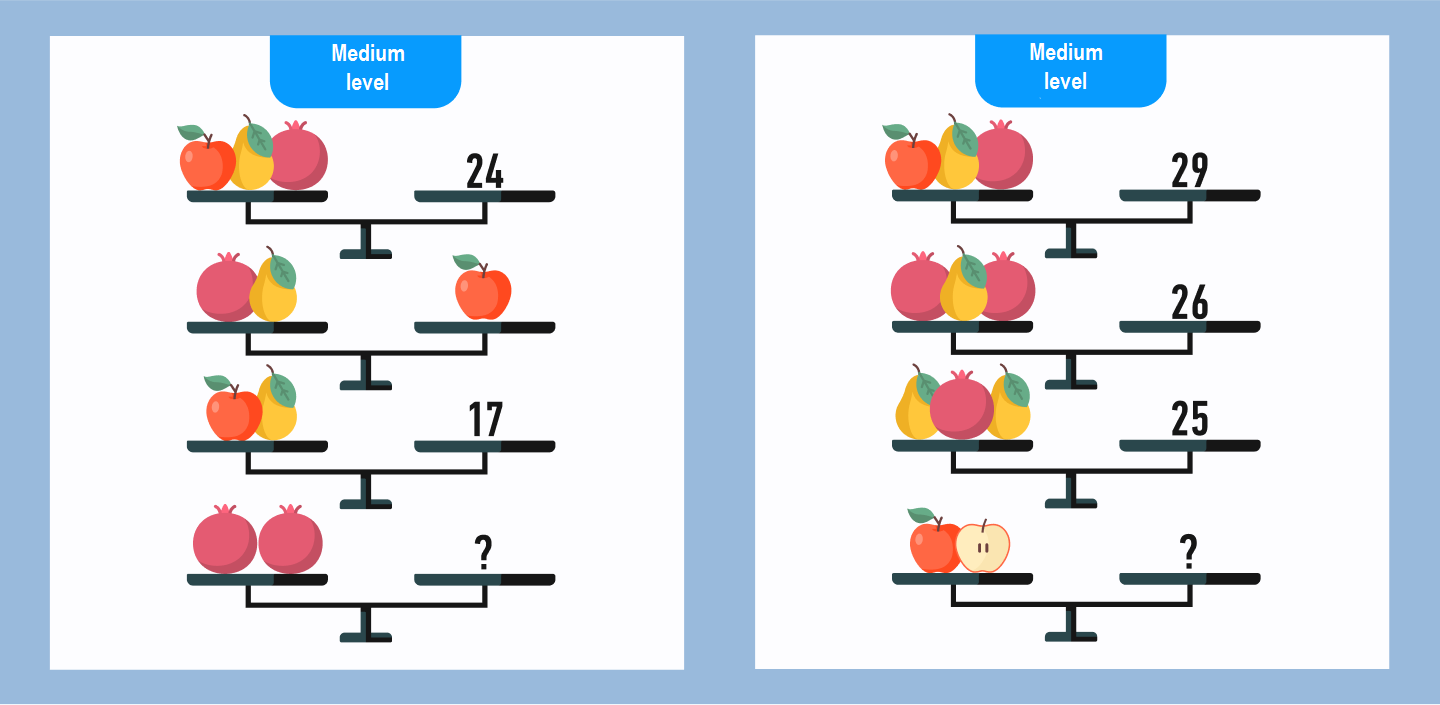
Here, the correct answers are:
- 14 for the left puzzle
- 18 for the right puzzle
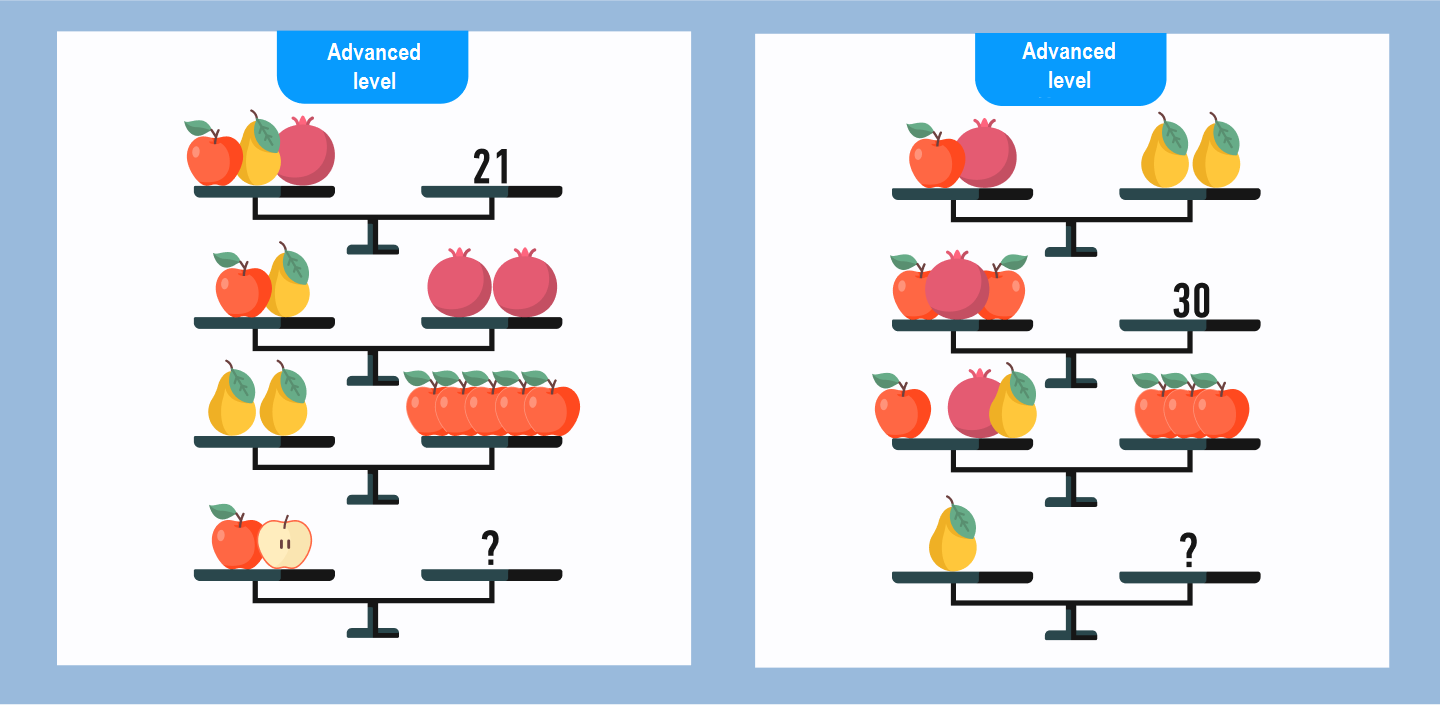
Here, the correct answers are:
- 6 for the left puzzle
- 9 for the right puzzle.
Puzzle #2
In another puzzle, we can see butterflies instead of specific numbers. Each butterfly has a corresponding number. You need to determine these numbers and solve the puzzle.

Let’s take a look at the first (upper left) “card”.
Two blue butterflies + two red ones make 58. Two red ones + two green ones are 56. Three blue ones are equal to 39. We need to solve the example with red + blue + green + blue ones.
It is easy to start with the third equality — 39:3 = 13. So, the number 13 corresponds to the blue butterfly.
13 * 2 + two red butterflies make 58. So, the two red ones are 58 – 26 = 32. Hence, one red butterfly is equal to 32: 2 = 16.
Now let’s count what the green butterfly is equal to. To do this, let’s turn to the second equality and substitute the values we already know into it: 32 + 2x = 56 → 2x = 56 – 32 = 24. So, x = 12.
Finally, we need to put the numbers into the last example: 16 + 13 – 12 + 13 = 30.
Try to solve the rest of the cards yourself.
Here, the correct answers are:
Card #1 — 30
Card #2 — 37
Card #3 — 10
Card #4 — 37
Card #5 — 62
Card #6 — 24
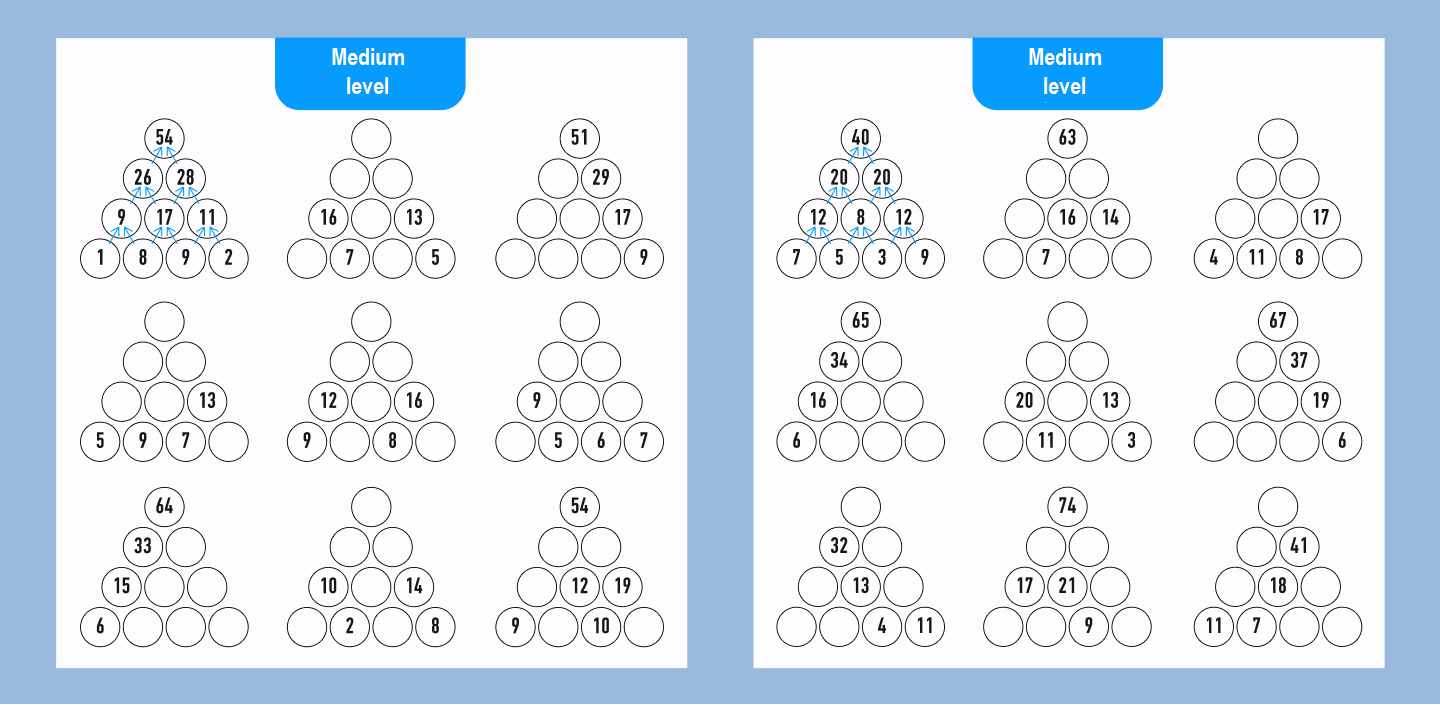
Puzzle #3
The third type of puzzles with pyramids is based only on the knowledge of arithmetic, with nothing to puzzle over.

Let’s see how to solve it, using the example of the second pyramid with numbers 1, 4, and 11.
It is necessary to substitute the numbers in the pyramid so that two neighboring ones in a row make the number above them.
Let’s start with the second level of the pyramid: 4 + x = 11 (the number in the top level), therefore, x = 7. At the lower level of the pyramid, let’s count the number that needs to be added to 1 to get 4. This is 3. Thus, only one circle remains empty: 7 – 3 = 4.
We suggest you solve the rest of the pyramids yourself.
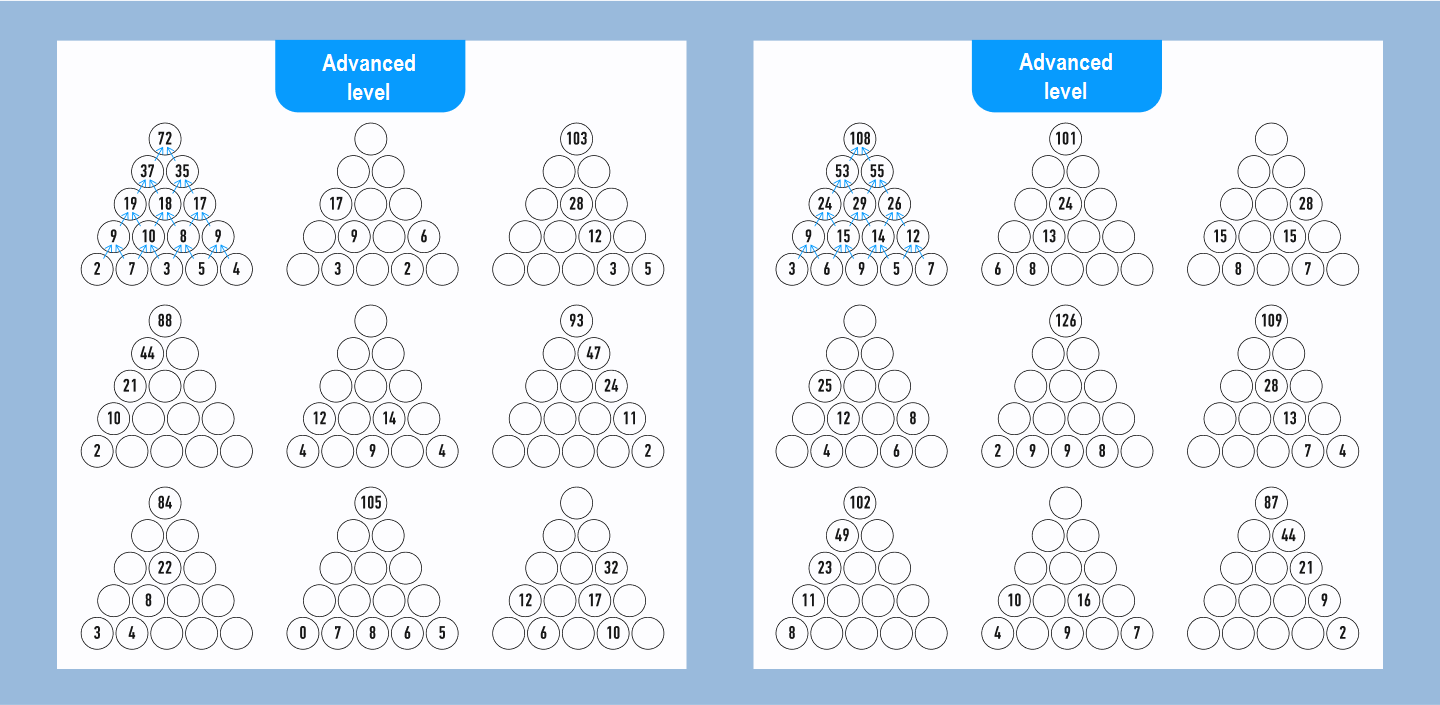
If you have successfully coped with the pyramids for beginners, we suggest you try your hand at intermediate and advanced level puzzles!
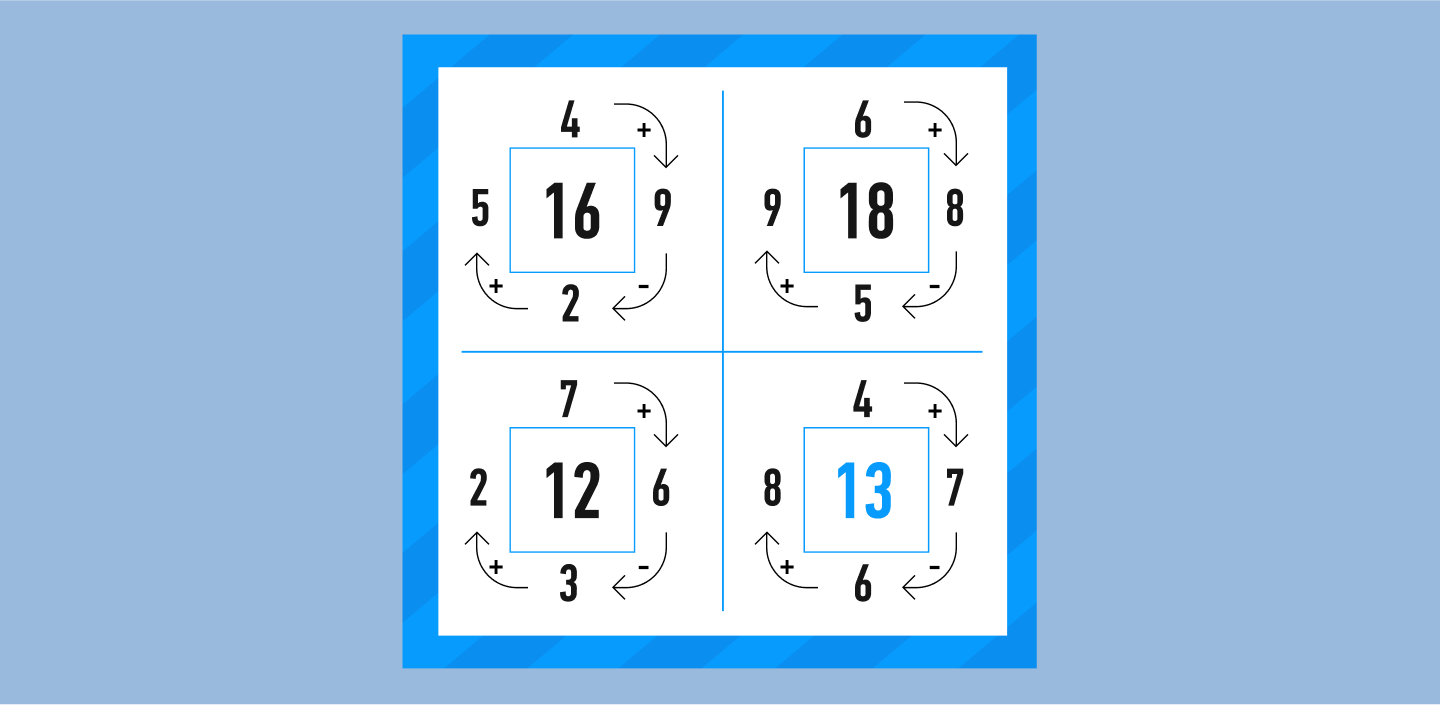
Puzzle #4
One more type of math puzzle trains self-organization and attention, as the precise selection is the only way to solve them.

In the first example, which is relatively simple, we need to define a sequence of mathematical operations with the supplied four numbers, which results in the number in the center. The order of addition/subtraction is the same in all examples — having caught the correct sequence, you need to solve the last example.
If we take a close look at the numbers, we can notice that in the first three cases, we get the center number by using the sequential combination of “+”, “-“, “+” and moving clockwise:
- 4+ 9 – 2 + 5,
- 6 + 8 – 5 + 9,
- 7 + 6 – 3 + 2.
We solve our example using the same scheme: 4 + 7 – 6 + 8 = 13.
Try to solve the next two puzzles yourself.


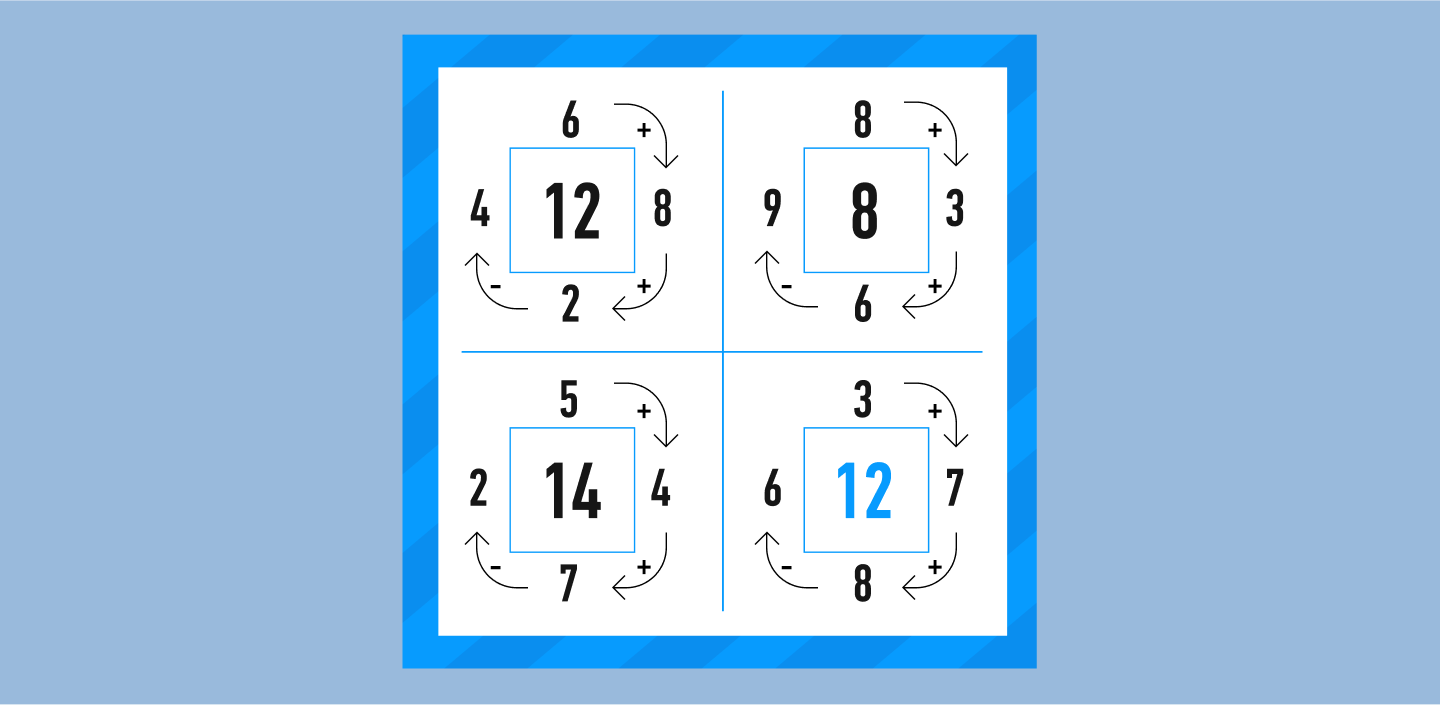
Like any learning task, math puzzles come in beginner, intermediate, and advanced levels. Knowing the principle of solving easy puzzles, you can move on to more complex ones up to the advanced level.
The more exercises children have, the easier it will be for them to cope with the highest level tasks and feel more confident at maths lessons at school.
Mathematical puzzles, games, and tasks help you learn to operate with numbers, think critically, reason, analyze and make your own decisions and choices. Within EdCraft, we can offer you a lot of math games, number puzzles and tasks for preschoolers, elementary and secondary school students. Our tasks look like funny interactive games for children of different ages, teaching them to solve logical and mathematical problems, helping the heroes to cope with their problems, and developing interesting plots.

new engaging articles



